비트(bit)란?
값을 저장할 수 있는 최소 단위
비트는 '전기가 흐르는 상태인 1(ON)' 또는 '전기가 흐르지 않는 상태인 0(OFF)'을 값으로 가지며, 컴퓨터는 이러한 비트 여러 개를 연결하여 온갖 데이터를 표현할 수 있다. 흔히 "컴퓨터는 0과 1 밖에 모른다"라고 하는데 텍스트, 이미지, 영상 등 어떤 데이터든 간에 그 근본을 파헤쳐보면 비트를 기반으로 구성되어 있기 때문이다.
참고: 프로그래밍에서 0은 거짓(false)을 의미하고, 1은 참(true)을 의미하는 논리적인 표현으로 사용하기도 한다.
바이트(byte)
우리가 흔히 사용하는 숫자는 10개이기 때문에, 1~2개의 적은 숫자만으로도 꽤나 유의미한 표현을 할 수 있다.
하지만 컴퓨터는 0과 1만 사용하기 때문에 1~2개의 비트만으로는 표현할 수 있는 정보가 매우 제한적이다.
때문에 컴퓨터는 8개의 비트를 묶어서 데이터의 기본 단위로 사용하며, 이를 바이트라고 부른다.
진법이란?
진법은 임의의 숫자를 사용하여 수를 표현하는 방식이다.
우리가 일상적으로 사용하고 있는 10진법은 0부터 9까지 10개의 숫자를 이용해서 수를 표현하기 때문에 10진법인 것이다.
마찬가지로 컴퓨터는 0과 1로만 수를 표현할 수 있기 때문에 컴퓨터가 수를 표현하는 방식을 2진법이라고 부른다.
0과 1로만 모든 수를 표현해야 하기 때문에 자릿수가 많이 필요하다는 점을 제외하면 10진법과 동일하다.

10진법에서 한 자릿수가 9를 넘어가면 다음 자릿수를 하나 더한 후 0으로 돌아가는 것처럼,
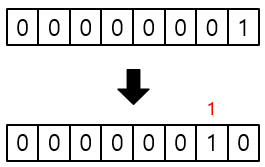
2진법에서도 한 자릿수가 1을 넘어가면 다음 자릿수를 하나 더한 후 0으로 되돌아간다.
이외에도 자릿수가 너무 길어진다는 2진법의 단점을 보완하기 위해 8진법이나 16진법이 고안되었다.
8진법은 0~7까지의 숫자를 사용하고, 16진법은 0~9까지의 숫자와 A~F까지의 문자를 사용한다.
예를 들어 10진수 '11'은 2진수로는 '1011', 8진수로는 '13', 16진수로는 'B'이다.
진법 변환하기
2진수를 8진수, 16진수로 변환하기
8과 16은 2의 거듭제곱이기 때문에 2진수에서 8진수나 16진수로 변환하는 것은 어렵지 않다.
8은 2^3이므로 2진수 3자리를 8진수 1자리로 교체하면 되고, 16은 2^4이므로 4자리를 교체하면 된다.
반대로 8진수나 16진수를 2진수로 변환하는 것은 위의 과정을 거꾸로 하면 된다.

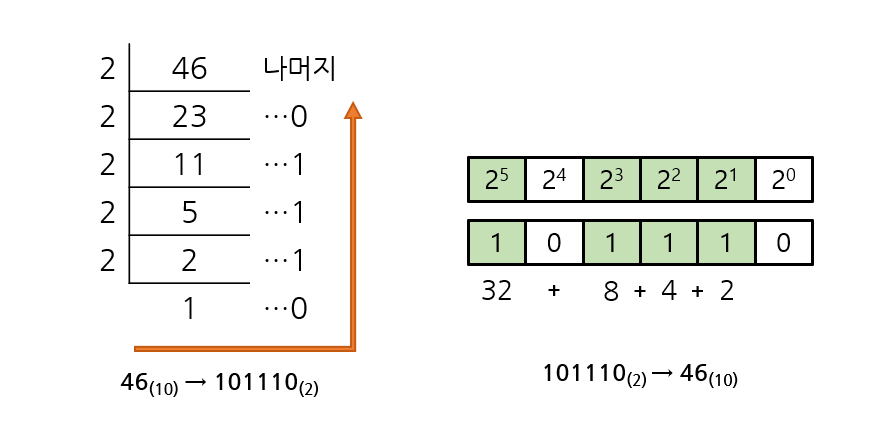
10진 정수의 n진법 변환
10진 정수를 n진 정수로 변환하려면, 우선 해당 수를 몫이 n보다 작아질 때까지 n으로 계속 나눠야 한다.
그러다 몫이 n보다 작아지면, 그 몫과 이전에 계산했던 나머지를 아래서 위로 순서대로 적으면 된다.
반대로 n진 정수를 10진 정수로 변환하려면, 각 자릿수에 n의 거듭제곱을 곱한 후에 더하면 된다.
아래의 2진법 변환 예시를 참고하면 쉽게 이해할 수 있을 것이다.
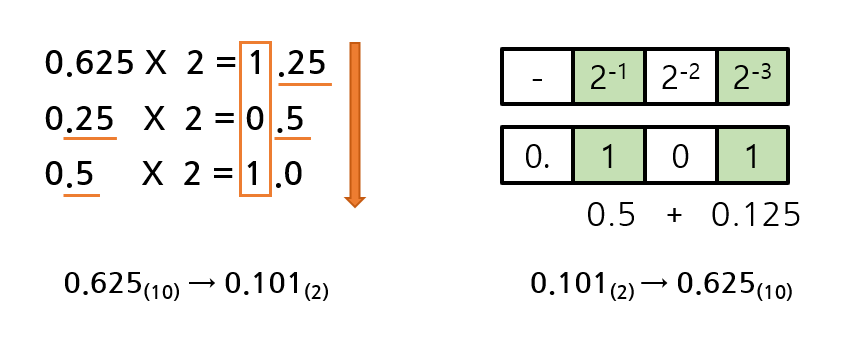
10진 실수의 n진법 변환
실수의 변환 방식은 정수의 변환 방식과 크게 다르지 않다.
단지 10진 정수는 각 자릿수가 10이 몇 번 곱해졌는지 나타낸다면, 10진 소수는 몇 번 나눠졌는지 나타낸다.
때문에 10진 실수를 n진 실수로 변환하려면, 반대로 n을 계속 곱해주면 된다.
마찬가지로 n진 실수를 10진 실수로 변환하려면, 각 자릿수에 n의 거듭제곱을 나눈 후 더해주면 된다.
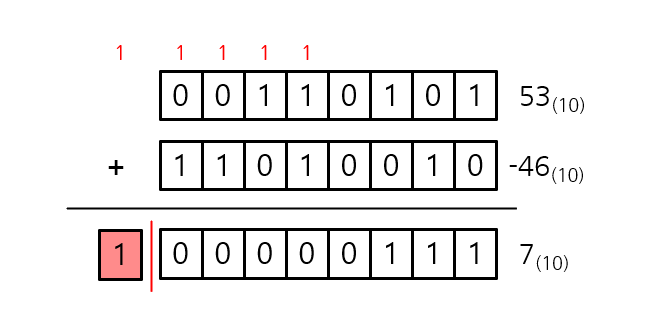
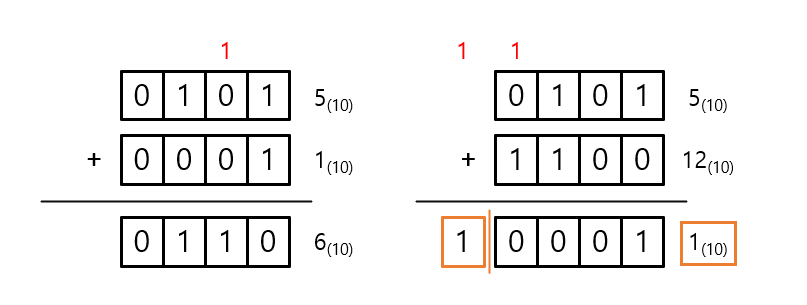
2진수의 덧셈과 뺄셈
2진수의 덧셈
2진수의 덧셈은 우리가 일반적으로 10진수를 덧셈하는 것과 크게 다르지 않다.
오히려 0과 1 밖에 없기 때문에 10진수끼리 덧셈하는 것보다 더 간단하게 덧셈을 할 수 있다.
참고: 컴퓨터가 2진수 연산을 진행할 때 연산 결과가 정해진 범위를 초과하면, 초과된 자릿수를 버린다는 사실을 기억해 두면 좋다.
그렇다면 2진수의 뺄셈은 어떻게 하는 것일까?
일반적인 10진수 뺄셈처럼 계산하는 방법도 있지만, 컴퓨터는 절댓값이 같은 음수를 덧셈하는 방법을 사용한다.
2진수의 뺄셈을 이해하려면 먼저 컴퓨터가 어떻게 음수를 표현하는 지부터 알아야 한다.
2진수의 음수 표현
앞서 언급했듯이 컴퓨터는 덧셈만 가능하기 때문에, 뺄셈을 하기 위해 음수를 더하는 방법을 사용한다.
때문에 컴퓨터는 수를 저장할 때 저장 공간의 절반은 양수, 나머지 절반은 음수를 저장한다.
참고: 2진수에서 가장 왼쪽의 최상위 비트를 부호 비트(sign bit)라고 한다. 부호 비트의 값이 0이면 양수, 1이면 음수를 의미한다.
부호 비트를 기준으로 절반을 나누기 때문에 0은 양수의 범위에 들어간다. 그래서 양수가 음수보다 1개 적게 저장된다.
이때 컴퓨터는 부호의 개념을 대체하여 음수를 표현하기 위해 보수법이라는 방식을 사용한다.
2진수에서 보수는 양수와 대응하여 음수를 표현하는 수로, 보수법에는 '1의 보수법'과 '2의 보수법'이 있다.
1의 보수법
1의 보수법은 단순히 양의 2진수 값을 전부 반대로 뒤집으면 된다. 예를 들어 '0101'(5)의 보수는 '1010'(-5)이다.
간단하지만 이 방식을 사용하면 0이 두 개가 생기기 때문에 주로 2의 보수법을 사용한다. (0000 : +0, 1111 : -0)
2의 보수법
2의 보수를 구하는 두 가지 방법이 있다.
첫 번째, 1의 보수를 구한 후에 1을 더해주는 방법

두 번째, 2진수로 변환한 후에 가장 처음 만나는 1의 왼쪽에 있는 비트를 전부 1의 보수로 바꿔주는 방법

2진수의 뺄셈
이제 2진수로 음수를 표현하는 방법을 알게 되었으니, 덧셈을 통해 뺄셈과 동일한 연산을 할 수 있게 되었다.
위의 내용들을 바탕으로 아래의 예시를 보면 쉽게 이해할 수 있을 것이다.